Rodin User’s Handbook v.2.8: Introducing user-defined types

2.5.4 Introducing user-defined types

We can introduce our own new types simply by giving such types a name. This is done by adding the name of the type to the SETS section of a context. We will see how this is done in practice in the next section (2.6).

For instance, if we want to model different kind of fruits in our model, we might create the set $FRUITS$ . Then the identifier $FRUITS$ denotes the set of all elements of this type. Nothing more is known about $FRUITS$ unless we add further axioms. In particular, we do not know the cardinality (number of elements) of the set or even if it is finite.

$\includegraphics[width=7mm]{img/warning_64.png}$
Assume that we want to model $apples$ and $oranges$ which are sub-sets of $FRUITS$ . We do not need to introduce them in the SETS section of a context just because they are sets. Let’s imagine such a scenario where $apples$ and $oranges$ are modelled as types of their own (by declaring them in the SETS section). And we have two variables or constants $a$ and $o$ with $a\in apples$ and $o\in oranges$ . Then we cannot compare $a$ and $o$ with $a=o$ or $a\neq o$ . That would raise a type error because $=$ and $\neq$ expect the same type for the left and right expression.

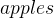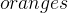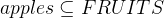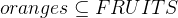If we want to model sub-sets $apples$ and $oranges$ as described above, we can add them as constants and state that $apples \subseteq FRUITS$ and $oranges \subseteq FRUITS$ . If apples and oranges are all fruits we want to model, we can assume 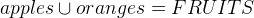$apples \cup oranges = FRUITS$ and if no fruit is both an apple and orange we can write 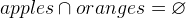$apples \cap oranges = \emptyset$ . 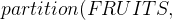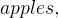A shorter way to express this is to say that apples and oranges constitute a partition of the fruits: 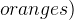$partition(FRUITS,$ $apples,$ $oranges)$ . 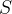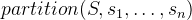In general, we can use the partition operator to express that a set $S$ is partitioned by the sets $s_1,\ldots ,s_ n$ with $partition(S,s_1,\ldots ,s_ n)$ . We use partitions in Section 2.6.2.1.

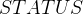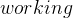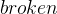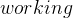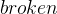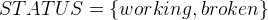Another typical usage for user defined data types are enumerated sets. These are sets where we know all the elements already. Let’s take a system which can be either working or broken. We model this by introducing a type $STATUS$ in the SETS section and two constants $working$ and $broken$ . We define that STATUS consists of exactly $working$ and $broken$ by $STATUS = \{ working,broken\}$ . 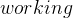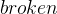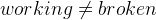Additionally, we have to say that $working$ and $broken$ are not the same by $working \neq broken$ .

If the enumerated sets gets larger, we need to state for every two element of the set that they are distinct. Thus, for a set of 10 constants, we’ll need 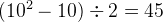$(10^2-10)\div 2 = 45$ predicates. Again, we can use the partition operator to express this in a more concise way:

$partition(STATUS,\{ working\} ,\{ broken\} )$

Rodin Handbook

2.5.4 Introducing user-defined types