Rodin User’s Handbook v.2.8: Operations on Sets

2.5.3 Operations on Sets

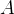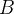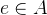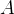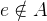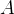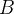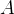Let’s assume that we have two sets $A$ and $B$ of the same type, e.g. sets of integers. Then we can check if an element $e$ is in it with the expression $e\in A$ (ASCII: e:A) or on if it is not in $A$ with $e\notin A$ (ASCII: e/:A). Expressing that all elements of $A$ are also elements of $B$ (i.e. $A$ is a subset of 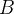$B$ ) can be done with the expression 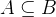$A\subseteq B$ (ASCII: A<:B). The negated form is 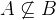$A\not\subseteq B$ (ASCII: A/<:B).

We can build the union 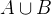$A\cup B$ , the intersection $A\cap B$ and the set subtraction 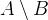$A\setminus B$ (ASCII: A\/B, A/\B and A\B). The set subtraction contains all elements that are in 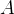$A$ but not in $B$ .

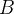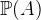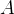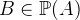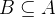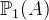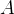The power set $\mathop {\mathbb P\hbox{}}\nolimits (A)$ (ASCII: POW(A)) is the set of all subsets of $A$ . Thus $B\in \mathop {\mathbb P\hbox{}}\nolimits (A)$ is equivalent to $B\subseteq A$ . $\mathop {\mathbb P\hbox{}}\nolimits _1(A)$ (ASCII: POW1(A)) is the set of all non-empty subsets of $A$ .

Rodin Handbook

2.5.3 Operations on Sets