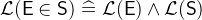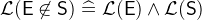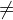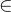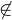Rodin User’s Handbook v.2.8: Predicates

3.3.2 Predicates

3.3.2.1 Logical primitives

$\mathord {\top }$	`true`	True
$\mathord {\bot }$	`false`	False

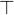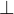Description: The predicates $\mathord {\top }$ and $\mathord {\bot }$ are the predicates that are true and false respectively.
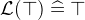
WD: $\mathcal{L}(\mathord {\top }) \mathrel {\widehat=}\mathord {\top }$
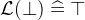
$\mathcal{L}(\mathord {\bot }) \mathrel {\widehat=}\mathord {\top }$

3.3.2.2 Logical operators

$\land$	`&`	Conjunction
$\lor$	`or`	Disjunction
$\mathbin \Rightarrow$	`=>`	Implication
$\mathbin \Leftrightarrow$	`<=>`	Equivalence
$\lnot$	`not`	Negation

Description

These are the usual logical operators.

Definition

The following truth tables describe the behaviours of these operators:

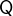
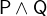
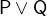
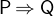
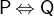
$\textsf{P}$	$\textsf{Q}$	$\textsf{P}\land \textsf{Q}$	$\textsf{P}\lor \textsf{Q}$	$\textsf{P}\mathbin \Rightarrow \textsf{Q}$	$\textsf{P}\mathbin \Leftrightarrow \textsf{Q}$
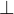
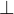
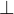
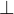
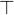
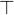
$\mathord {\bot }$	$\mathord {\bot }$	$\mathord {\bot }$	$\mathord {\bot }$	$\mathord {\top }$	$\mathord {\top }$
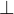
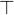
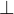
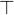
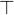
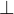
$\mathord {\bot }$	$\mathord {\top }$	$\mathord {\bot }$	$\mathord {\top }$	$\mathord {\top }$	$\mathord {\bot }$
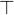
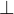
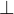
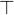
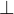
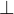
$\mathord {\top }$	$\mathord {\bot }$	$\mathord {\bot }$	$\mathord {\top }$	$\mathord {\bot }$	$\mathord {\bot }$
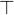
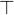
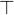
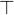
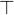
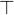
$\mathord {\top }$	$\mathord {\top }$	$\mathord {\top }$	$\mathord {\top }$	$\mathord {\top }$	$\mathord {\top }$

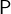
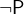
$\textsf{P}$	$\lnot \textsf{P}$
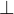
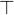
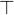
$\mathord {\bot }$	$\mathord {\top }$
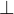
$\mathord {\top }$	$\mathord {\bot }$

Types

All arguments are predicates.

WD

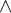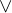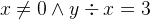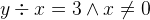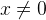Please note that the operators $\land$ and $\lor$ are not commutative because their well-definedness conditions distinguish between the first and second argument. Therefore, if their arguments have well-definedness conditions, the order matters. For example, $x\neq 0 \land y\div x=3$ is always well-defined, but $y\div x=3 \land x\neq 0$ still has the well-definedness condition $x\neq 0$ .

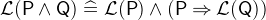
$\mathcal{L}(\textsf{P}\land \textsf{Q}) \mathrel {\widehat=}\mathcal{L}(\textsf{P}) \land (\textsf{P}\mathbin \Rightarrow \mathcal{L}(\textsf{Q}))$
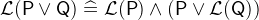
$\mathcal{L}(\textsf{P}\lor \textsf{Q}) \mathrel {\widehat=}\mathcal{L}(\textsf{P}) \land (\textsf{P}\lor \mathcal{L}(\textsf{Q}))$
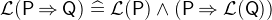
$\mathcal{L}(\textsf{P}\mathbin \Rightarrow \textsf{Q}) \mathrel {\widehat=}\mathcal{L}(\textsf{P}) \land (\textsf{P}\mathbin \Rightarrow \mathcal{L}(\textsf{Q}))$
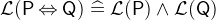
$\mathcal{L}(\textsf{P}\mathbin \Leftrightarrow \textsf{Q}) \mathrel {\widehat=}\mathcal{L}(\textsf{P}) \land \mathcal{L}(\textsf{Q})$
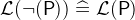
$\mathcal{L}(\lnot (\textsf{P})) \mathrel {\widehat=}\mathcal{L}(\textsf{P})$

3.3.2.3 Quantified predicates

$\forall$	`!`	Universal quantification
$\exists$	`#`	Existential quantification

Description

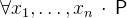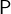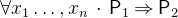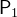The universal quantification $\forall x_1,\ldots ,x_ n~ \mathord {\mkern 1mu\cdot \mkern 1mu}~ \textsf{P}$ is true if $\textsf{P}$ is satisfied for all possible values of $x_1\ldots ,x_ n$ . A usual pattern for quantification is $\forall x_1\ldots ,x_ n~ \mathord {\mkern 1mu\cdot \mkern 1mu}~ \textsf{P}_1\mathbin \Rightarrow \textsf{P}_2$ where $\textsf{P}_1$ is used to specify the types of the identifiers.

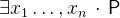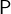The existential quantification $\exists x_1\ldots ,x_ n~ \mathord {\mkern 1mu\cdot \mkern 1mu}~ \textsf{P}$ is true if a value of $x_1\ldots ,x_ n$ exists such that $\textsf{P}$ is satisfied.

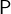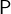The types of all identifiers $x_1\ldots ,x_ n$ must be inferable by $\textsf{P}$ . They can be referenced in $\textsf{P}$ .

Types

The quantifiers and the 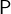$\textsf{P}$ are predicates.

WD

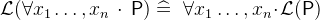
$\mathcal{L}(\forall x_1\ldots ,x_ n~ \mathord {\mkern 1mu\cdot \mkern 1mu}~ \textsf{P}) \mathrel {\widehat=}~ \forall x_1\ldots ,x_ n \mathord {\mkern 1mu\cdot \mkern 1mu}\mathcal{L}(\textsf{P})$
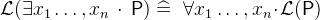
$\mathcal{L}(\exists x_1\ldots ,x_ n~ \mathord {\mkern 1mu\cdot \mkern 1mu}~ \textsf{P}) \mathrel {\widehat=}~ \forall x_1\ldots ,x_ n \mathord {\mkern 1mu\cdot \mkern 1mu}\mathcal{L}(\textsf{P})$

3.3.2.4 Equality

$=$	`=`	equality
$\neq$	`/=`	inequality

Description: Checks if both expressions are or are not equal.
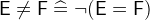
Definition: $\textsf{E}\neq \textsf{F}\mathrel {\widehat=}\lnot ( \textsf{E}=\textsf{F})$
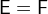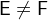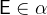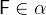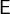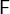Types: $\textsf{E}= \textsf{F}$ and $\textsf{E}\neq \textsf{F}$ are predicates with $\textsf{E}\in \alpha$ and $\textsf{F}\in \alpha$ , i.e. $\textsf{E}$ and $\textsf{F}$ must have the same type.
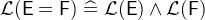
WD: $\mathcal{L}(\textsf{E}= \textsf{F}) \mathrel {\widehat=}\mathcal{L}(\textsf{E}) \land \mathcal{L}(\textsf{F})$
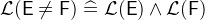
$\mathcal{L}(\textsf{E}\neq \textsf{F}) \mathrel {\widehat=}\mathcal{L}(\textsf{E}) \land \mathcal{L}(\textsf{F})$

3.3.2.5 Membership

$\in$	`:`	set membership
$\not\in$	`/:`	negated set membership

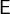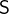Description: Checks if an expression $\textsf{E}$ denotes an element of a set $\textsf{S}$ .
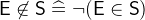
Definition: $\textsf{E}\not\in \textsf{S}\mathrel {\widehat=}\lnot (\textsf{E}\in \textsf{S})$
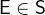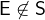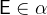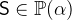Types: $\textsf{E}\in \textsf{S}$ and $\textsf{E}\not\in \textsf{S}$ are predicates with $\textsf{E}\in \alpha$ and $\textsf{S}\in \mathop {\mathbb P\hbox{}}\nolimits (\alpha )$ .
WD: $\mathcal{L}(\textsf{E}\in \textsf{S}) \mathrel {\widehat=}\mathcal{L}(\textsf{E}) \land \mathcal{L}(\textsf{S})$
$\mathcal{L}(\textsf{E}\not\in \textsf{S}) \mathrel {\widehat=}\mathcal{L}(\textsf{E}) \land \mathcal{L}(\textsf{S})$

Rodin Handbook