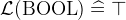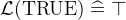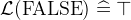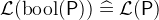Rodin User’s Handbook v.2.8: Booleans

3.3.3 Booleans

$\mathord {\mathrm{BOOL}}$	`BOOL`	Boolean values
$\mathord {\mathrm{TRUE}}$	`TRUE`	Boolean true
$\mathord {\mathrm{FALSE}}$	`FALSE`	Boolean false
$\mathop {\mathrm{bool}}\nolimits$	`bool`	Convert a predicate into a Boolean value

Description

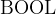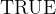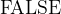$\mathord {\mathrm{BOOL}}$ is a pre-defined carrier set that contains the constants $\mathord {\mathrm{TRUE}}$ and $\mathord {\mathrm{FALSE}}$ .

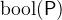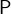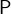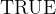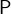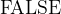$\mathop {\mathrm{bool}}\nolimits (\textsf{P})$ denotes the Boolean value of a predicate $\textsf{P}$ . If $\textsf{P}$ is true, the expression is $\mathord {\mathrm{TRUE}}$ . If $\textsf{P}$ is false, the expression is $\mathord {\mathrm{FALSE}}$ .

Definition

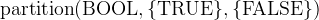
$\mathrm{partition}(\mathord {\mathrm{BOOL}},\{ \mathord {\mathrm{TRUE}}\} ,\{ \mathord {\mathrm{FALSE}}\} )$
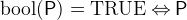
$\mathop {\mathrm{bool}}\nolimits (\textsf{P})=\mathord {\mathrm{TRUE}}\mathbin \Leftrightarrow \textsf{P}$

Types

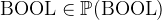
$\mathord {\mathrm{BOOL}}\in \mathop {\mathbb P\hbox{}}\nolimits (\mathord {\mathrm{BOOL}})$
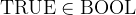
$\mathord {\mathrm{TRUE}}\in \mathord {\mathrm{BOOL}}$
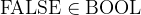
$\mathord {\mathrm{FALSE}}\in \mathord {\mathrm{BOOL}}$
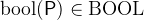$\mathop {\mathrm{bool}}\nolimits (\textsf{P})\in \mathord {\mathrm{BOOL}}$ with $\textsf{P}$ being a predicate.

WD

$\mathcal{L}(\mathord {\mathrm{BOOL}}) \mathrel {\widehat=}\mathord {\top }$
$\mathcal{L}(\mathord {\mathrm{TRUE}}) \mathrel {\widehat=}\mathord {\top }$
$\mathcal{L}(\mathord {\mathrm{FALSE}}) \mathrel {\widehat=}\mathord {\top }$
$\mathcal{L}(\mathop {\mathrm{bool}}\nolimits (\textsf{P})) \mathrel {\widehat=}\mathcal{L}(\textsf{P})$

Rodin Handbook

3.3.3 Booleans