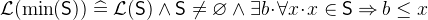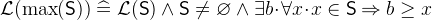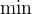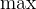Rodin Handbook
This work is sponsored by the Deploy Project
This work is sponsored by the ADVANCE Project
This work is licensed under a Creative Commons Attribution 3.0 Unported License
3.3.6 Arithmetic
3.3.6.1 Sets of numbers
|
INT |
Integers |
|
NAT |
Natural numbers, starting with 0 |
|
NAT1 |
Natural numbers, starting with 1 |
|
.. |
Range of numbers |
- Description
The set of all integers is denoted by
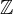 . It contains all elements of the type. The two subsets
. It contains all elements of the type. The two subsets 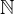 and
and 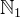 contain all elements greater than or equal to 0 and 1 respectively. The range of numbers between
contain all elements greater than or equal to 0 and 1 respectively. The range of numbers between  and
and 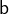 is denoted by
is denoted by 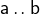 .
. - Definition
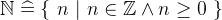
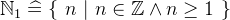
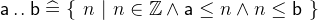
- Types
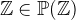
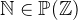
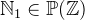
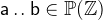 with
with 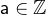 and
and 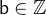
- WD
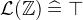
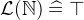
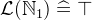
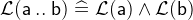
3.3.6.2 Arithmetic operations
|
+ |
Addition |
|
- |
Subtraction or unary minus |
|
* |
Multiplication |
|
/ |
Integer division |
|
mod |
Modulo |
|
^ |
Exponentiation |
- Description
These are the usual arithmetic operations.
- Definition
Addition, subtraction and multiplication behave as expected.
The division is defined in a way that
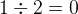 and
and 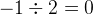 :
: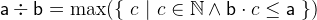 for
for 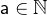 and
and 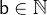
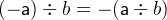

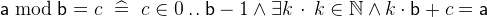
- Types
With
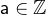 ,
, 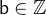 for each operator
for each operator  of
of  ,
,  ,
,  ,
, 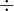 ,
, 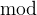 :
: 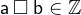

- WD
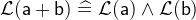
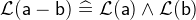
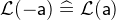
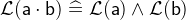
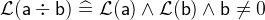
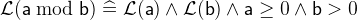
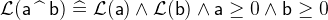
3.3.6.3 Minimum and Maximum
|
min |
Minimum |
|
max |
Maximum |
- Description
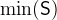 and
and 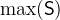 denotes the smallest and largest number in the set of integers
denotes the smallest and largest number in the set of integers 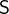 respectively.
respectively. The minimum and maximum are only defined if such a number exists.
- Definition
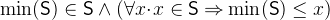
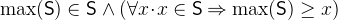
- Types
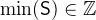 and
and 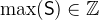 with
with 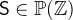 .
. - WD