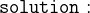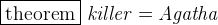Rodin User’s Handbook v.2.8: The Final Context

2.6.3 The Final Context

CONTEXT

agatha

SETS

$\tt persons$

CONSTANTS

$\tt Agatha$
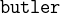
$\tt butler$
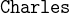
$\tt Charles$
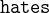
$\tt hates$
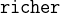
$\tt richer$
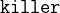
$\tt killer$

AXIOMS

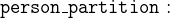
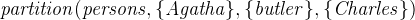
$\tt person\_ partition :$: $\it partition(persons, \{ Agatha\} , \{ butler\} , \{ Charles\} )$
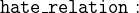
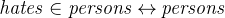
$\tt hate\_ relation :$: $\it hates \in persons \mathbin \leftrightarrow persons$
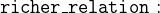
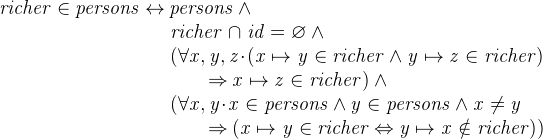
$\tt richer\_ relation :$: $\it richer \in persons \mathbin \leftrightarrow persons \land \\ \hspace*{2.5 cm} richer \mathbin {\mkern 1mu\cap \mkern 1mu}id = \emptyset \land \\ \hspace*{2.5 cm} (\forall x,y,z \mathord {\mkern 1mu\cdot \mkern 1mu}( x\mapsto y\in richer \land y\mapsto z\in richer) \\ \hspace*{3.2 cm}\mathbin \Rightarrow x\mapsto z\in richer) \land \\ \hspace*{2.5 cm} (\forall x,y \mathord {\mkern 1mu\cdot \mkern 1mu}x\in persons \land y\in persons \land x\neq y \\ \hspace*{3.2 cm}\mathbin \Rightarrow (x\mapsto y\in richer \mathbin \Leftrightarrow y\mapsto x \notin richer))$
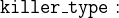
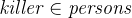
$\tt killer\_ type :$: $\it killer \in persons$
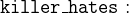
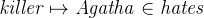
$\tt killer\_ hates :$: $\it killer \mapsto Agatha \in hates$
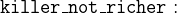
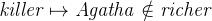
$\tt killer\_ not\_ richer :$: $\it killer \mapsto Agatha \notin richer$
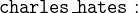
$\tt charles\_ hates :$: $\it hates[\{ Agatha\} ] \mathbin {\mkern 1mu\cap \mkern 1mu}hates[\{ Charles\} ] = \emptyset$
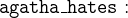
$\tt agatha\_ hates :$: $\it hates[\{ Agatha\} ] = persons \setminus \{ butler\}$
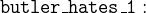
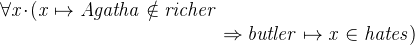
$\tt butler\_ hates\_ 1 :$: $\it \forall x\mathord {\mkern 1mu\cdot \mkern 1mu}( x\mapsto Agatha \notin richer \\ \hspace*{3.5 cm}\mathbin \Rightarrow butler\mapsto x \in hates)$
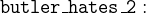
$\tt butler\_ hates\_ 2 :$: $\it hates[\{ Agatha\} ] \subseteq hates[\{ butler\} ] \land \\ \hspace*{3,2 cm} (\forall x\mathord {\mkern 1mu\cdot \mkern 1mu}x\in persons \mathbin \Rightarrow hates[\{ x\} ] \neq persons)$
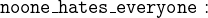
$\tt noone\_ hates\_ everyone :$: $\it \forall x \mathord {\mkern 1mu\cdot \mkern 1mu}x \in persons \land hates[\{ x\} ] \neq persons$
$\tt solution :$: $\it \fbox{theorem} ~ killer = Agatha$

END

Rodin Handbook

2.6.3 The Final Context