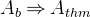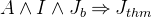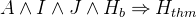Rodin User’s Handbook v.2.8: Theorems

Rodin Handbook

This work is sponsored by the Deploy Project

This work is sponsored by the ADVANCE Project

Creative Commons License

Creative Commons License

This work is licensed under a Creative Commons Attribution 3.0 Unported License

Theorems

Rodin User’s Handbook v.2.8

3.2.6 Theorems

Axioms, invariants and guards can be marked as theorems. This means that the validity of the theorems must be proven from the axioms, invariants or guards declared before the theorem.

Sometimes an axiom/invariant/guard marked as theorem is also called a derived axiom/invariant/guard.

3.2.6.1 Axioms

For an axiom 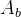$A_{thm}$ , $A_ b$ denotes (the conjunction of) all axioms declared in extended contexts and the axioms already declared in the current context before the axiom in question.

	An axiom as theorem
Name	label/THM
Goal	$A_ b \mathbin \Rightarrow A_{thm}$

3.2.6.2 Invariants

For an invariant 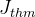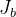$J_{thm}$ , $J_ b$ denotes (the conjunction of) all the model’s invariants declared before the theorem.

	An invariant as theorem
Name	label/THM
Goal	$A \land I \land J_ b \mathbin \Rightarrow J_{thm}$

3.2.6.3 Guards

For a guard 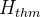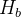$H_{thm}$ , $H_ b$ denotes (the conjunction of) all the event’s guards declared before the theorem.

	A guard as theorem
Name	label/THM
Goal	$A \land I \land J \land H_ b \mathbin \Rightarrow H_{thm}$

Rodin User’s Handbook v.2.8 : Reference : Event-B’s modelling notation : Theorems