Rodin Handbook
This work is sponsored by the Deploy Project
This work is sponsored by the ADVANCE Project
This work is licensed under a Creative Commons Attribution 3.0 Unported License
3.2.2 Substitutions
We use the notation ![$P[E/x]$](images/img-0522.png) for a substitution of all free occurrences of the variable
for a substitution of all free occurrences of the variable 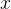 in
in 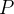 by the expression
by the expression 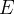 . Several substitutions can be performed simultaneously with
. Several substitutions can be performed simultaneously with  . In particular, we use the syntax
. In particular, we use the syntax ![$P[\mathbf{x}’/\mathbf{x}]$](images/img-0525.png) to denote the substitution of each identifier
to denote the substitution of each identifier 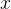 in the sequence
in the sequence 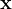 by
by 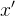 . For more information on free identifiers, see Section 3.3.1.3.
. For more information on free identifiers, see Section 3.3.1.3.
Examples:
![$(x>y)[5+2/y]$](images/img-0528.png) corresponds to the predicate
corresponds to the predicate 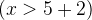 .
. ![$(x>y)[2\cdot y/x,5+2/y]$](images/img-0530.png) corresponds to the predicate
corresponds to the predicate 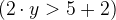 .
. ![$(\exists x \mathord {\mkern 1mu\cdot \mkern 1mu}x\in S \land x>y)[2\cdot y/x,5+2/y]$](images/img-0532.png) corresponds to the predicate
corresponds to the predicate 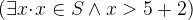 , because the
, because the 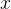 is a quantified variable (i.e. it is not a free variable).
is a quantified variable (i.e. it is not a free variable). For a sequence
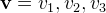 the predicate
the predicate ![$(v_1\subseteq v_2\land v_3\in v_1)[\mathbf{v}’/\mathbf{v}]$](images/img-0535.png) corresponds to
corresponds to 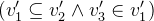 .
.