Rodin Handbook
This work is sponsored by the Deploy Project
This work is sponsored by the ADVANCE Project
This work is licensed under a Creative Commons Attribution 3.0 Unported License
3.3.8 Assignments
3.3.8.1 Deterministic Assignments
|
:= |
deterministic assignment |
- Description
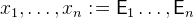 assigns the expressions
assigns the expressions 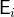 to the variable
to the variable 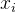 , with
, with 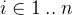 . All
. All 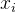 must be distinct identifiers that refer to variables of the concrete machine.
must be distinct identifiers that refer to variables of the concrete machine. There is a special form of the assignment which uses a relational overwrite:
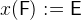 .
. - Definition
The before-after-predicate of
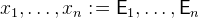 is
is .
. This assignment is equivalent to
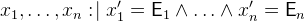 .
. The special form for this assignment is:
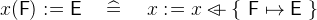
- Types
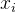 and
and 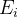 must have the same type:
must have the same type: 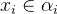 and
and 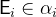 for
for 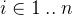 .
. - WD
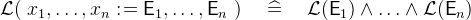
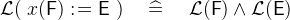
3.3.8.2 Non-deterministic assignment with before-after-predicate
|
:| |
non-deterministic assignment with a before-after-predicate |
- Description
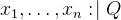 assigns any value to the variables
assigns any value to the variables  such that the the before-after-predicate
such that the the before-after-predicate 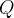 is fulfilled. Each
is fulfilled. Each 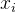 is an identifier that refers to a variable of the concrete machine.
is an identifier that refers to a variable of the concrete machine. All free identifiers in
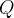 must be constants, concrete parameters, concrete variables or primed versions of the modified variables (
must be constants, concrete parameters, concrete variables or primed versions of the modified variables ( ).
). This is the most general form of assignment. All other assignments can be converted to this.
- Definition
The before-after-predicate is
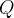 .
. - Types
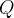 is a predicate and all
is a predicate and all 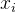 and
and 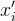 must have the same type:
must have the same type: 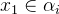 and
and 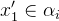 for
for 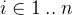 .
. - WD

- Feasibility
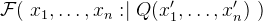

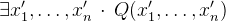
3.3.8.3 Non-deterministic assignment by sets
|
:: |
non-deterministic assignment of a set member |
- Description
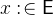 assigns any value of the set
assigns any value of the set 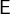 to the variable
to the variable 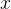 .
. 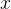 is an identifier that refers to a variable of the concrete machine.
is an identifier that refers to a variable of the concrete machine. All free identifiers in
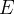 must be constants, concrete variables or concrete parameters.
must be constants, concrete variables or concrete parameters. - Definition
The before-after-predicate is
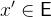 .
.
The assignment is equivalent to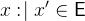 .
. - Types
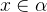 and
and 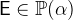
- WD
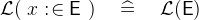
- Feasibility