Introduction
ProB is a graphical animator and model checker for the B method. The ProB homepage is at https://prob.hhu.de/w/, where precompiled binaries, installation instructions and documentation are available.
Important notice
If you find a problem with ProB or this documentation please let us know. We are happy to receive suggestions for improvements to ProB or the documentation. You can submit bug reports on our issue tracker. You can also post a question in our prob-users group or send an email to Michael Leuschel.
ProB 2.0 Java API Documentation
Introduction
For developers who want to build specialized tools on top of ProB, we have prepared comprehensive documentation of the ProB Java API together with a template that enables a quick start.
Acknowledgements
Parts of this document were taken from the ProB wiki, which contain contributions from a lot of people. We would like to thank Michael Birkhoff, Ivaylo Dobrikov, Rene Goebbels, Dominik Hansen, Philipp Körner, Sebastian Krings, Lukas Ladenberger, Michael Leuschel, Daniel Plagge, and Harald Wiegard for their contributions to the documentation and ProB 2.0.
About ProB 2.0
We believe that any proof centric formal method must be complemented by animation and visualization to be useful because there are always properties of a model that cannot be covered by proof. In particular, a proof can guarantee that a model is internally consistent, but it cannot guarantee that this model is actually what its designer had in mind. Animation and visualization can help to review models.
ProB is a mature toolset that supports a whole range of different formalisms such as classical B, Event-B, CSP and Z. Previously, we developed a ProB plug-in to add animation and model checking to the Rodin platform. This plug-in was designed to be extensible using an abstraction called a command. A command encapsulates a call to the ProB CLI that is written in the Prolog language and the result of that call. The architecture was successfully used to build third-party tools on top of ProB. For instance, the UML-B Statechart animation plug-in uses ProB.
However, while the design was very flexible there were some abstractions that were missing. For instance, the API had no notion of a state space or a trace through the state space. Each tool that required one of these concepts had to reinvent them. Also, building tools on top of ProB was a task for a plug-in developer and it required a good deal of effort, i.e., one needs to know how to create an Eclipse plug-in. We wanted to introduce a more lightweight approach to allow an end user to customize the tool itself. In ProB 2.0 this can be done using Groovy as an embedded scripting language. Our major design principles for the new version of ProB were:
-
Embrace Groovy We try to make (almost) everything accessible to the scripting language. This is very important because it enables customization and extension of the tool from within the tool. Actually we even tried to go further by designing the tool as if it were a library for Groovy. This made a couple of extensions to ProB extremely easy. For instance, adding CSP support to the plug-in only took a few hours.
-
Add recurring abstractions: We have identified three main abstractions: model, state space and trace. The state space contains two further abstractions: a state and a transition. The model represents the static properties of a specification, i.e., its abstract syntax. For Event-B this could have been done using the Rodin abstractions, but we wanted to use Event-B and classical B uniformly. A trace consists of a list of transitions that have been executed in order.
-
Prefer immutability: This is more a implementation principle than a design principle but we think it is essential to prefer immutable objects wherever it is possible. If we add a new step to a trace, we do not change the trace but we generate a new trace. Because of the consistent use of immutable values, we can use structural sharing to avoid expensive copying.
Architecture
In this chapter we will give an overview of the tool’s architecture. First we will explain the base components and then we will explain how these components interact with each other.
Overview of the Components
The following diagram shows the architecture of ProB 2.0.
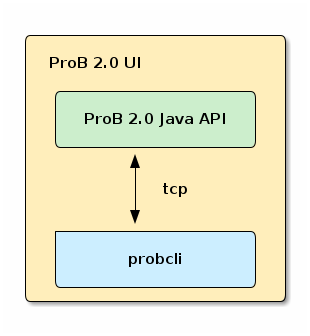
Prolog Binary
At the bottom layer it contains a platform specific binary. This binary is actually the same binary that is used from the shell (probcli). The binary is usually placed in a .prob folder in the user’s home directory. The binary communicates with the rest of the tool via tcp socket. While the current version does not support it, in principle the probcli does not have to run on the same computer as the rest of ProB. The probcli should not be integrated into other tools, use the Java API instead.
ProB 2.0 Java API
On top of the probcli binary we have a Java library that abstracts away the details of running animations. The library is the main part of ProB 2.0 and will be explained in more detail in the next chapter. It is important to notice that the library is only dependent on Java. There is no dependency to Eclipse or Rodin. The library is written in Java and Groovy. The Java API is a library hosted on Maven Central that can be included in other tools. Alternatively it is possible to extend the ProB 2.0 UI using its plug-in mechanism.
ProB 2.0 UI
On top of the Java API we developed a standalone JavaFX GUI, that is typically used by end users to run animations or model checking. The UI has a mechanism to add custom code.
Installation
You can use the ProB 2.0 archive. The easiest way is to use Gradle or Maven.
The artifact is providaed via Maven central The current developer Snapshot can be found in the Sonatype repository
The following listing shows an example Gradle build script that can be used as a template for builds. We have also prepared an example project that can be used as a template for a tool built on top of ProB 2.0.
apply plugin: 'java'
repositories {
mavenCentral()
maven {
name "sonatype"
url "https://oss.sonatype.org/content/repositories/snapshots/de/hhu/stups/"
}
}
dependencies {
compile "de.prob:de.prob.core.kernel:2.0.0" // replace version number
}
Low Level API
The ProB core has two different APIs. One is suited for high level usage and one directly interacts with the Prolog binary. The latter (low level) API is used to extend the functionality of ProB 2.0 and this is the API that we are introducing in this chapter. It is typically only used within the development team because it often requires changing parts of the Prolog kernel. However, it still may be useful to know where one can look for low level features. This is particulary helpful when some of the features are not yet accessible to a higher level API.
The low level API was introduced in the first version of ProB for Rodin and is still used in version 2.0. We use subclasses of the de.prob.animator.command.AbstractCommand class to interact with the ProB CLI that is written in the Prolog language. A command must implement two important methods: writeCommand and processResults. The basic idea is that we pass a command to the execute method of an instance of IAnimator. The IAnimator will call the command’s writeCommand method passing in an object that represents a Prolog query. It expects that the command will extend the Prolog query. The reason for this approach is that we want to combine multiple commands in a single call for efficiency reason and we have to take care to rename Prolog variables to prevent accidental unification between independent commands. For instance, a command could write the query foo(a,1,X) and a second command could write bar(X,Y). The combination foo(a,1,X), bar(X,Y) will probably yield a completely different result than executing them one after the other because X is unified. Typically this combination will fail. To prevent this, ProB automatically renames variables. In this instance, the combination would become foo(a,1,AX), bar(BX,BY).
After calling writeCommand, the query is sent to Prolog and executed. The animator thread blocks until it receives a result from Prolog. The relevant bits of the result are passed to the command’s processResult method. The command then proceeds to extract the information and store them in an appropriate format. This means that the command is a mutable object that also captures the result of a query. Usually commands provide a method to get the result as an object.
The following listing shows an example of a command that takes a state as an input and produces a list of transitions that represent the shortest (known) trace from the initial state. When called, it will produce a query such as prob2_find_trace(42,Trace). Prolog will bind the variable Trace to a list of prolog terms that represent the Transition objects in the StateSpace. These terms (tuples with the form op(TransitionId, Name, SourceId, DestinationId)) will be translated to Transition objects using the static method Transition.createTransitionFromCompoundPrologTerm when the processResult method is called. Finally we have a getter method that can be used to extract the result.
public class GetShortestTraceCommand extends AbstractCommand {
private static final String TRACE = "Trace";
private final State state;
private final List<Transition> transitions = new ArrayList<Transition>();
public GetShortestTraceCommand(final State state) {
this.state = state;
}
public void writeCommand(final IPrologTermOutput pto) {
pto.openTerm("find_trace_to_node");
pto.printAtomOrNumber(id.getId());
pto.printVariable(TRACE);
pto.closeTerm();
}
public void processResult(ISimplifiedROMap<String,PrologTerm> bindings){
PrologTerm trace = bindings.get(TRACE);
if (trace instanceof ListPrologTerm) {
for (PrologTerm term : (ListPrologTerm) trace) {
Transition transition = Transition.createTransitionFromCompoundPrologTerm(state.getStateSpace(),
(CompoundPrologTerm) term);
transitions.add(transition);
}
}
}
public List<Transition> getTransitions() {
return transitions;
}
}Figure 1 shows how commands are executed by ProB. Commands can be combined using ComposedCommand and executed via an instance of IAnimator. When the execute method returns, the commands have been processed and the results are ready.
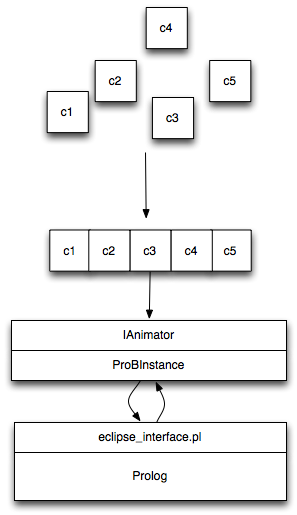
| Figure 1 is slightly outdated, the Prolog interface is located in prob2_interface.pl rather than eclipse_interface.pl. |
High Level API
We have introduced a high level API in ProB 2.0 which allows much nicer interaction with ProB. Before 2.0, all interaction was done using commands. There were no abstractions that represent typically used concepts such as a model, a state space, or a trace. Together with this high level API, we introduced a scripting interface that makes it very easy to tweak ProB and implement new features. Almost everything in ProB can be manipulated through Groovy scripts. This chapter will introduce the programmatic abstractions now available in ProB 2.0, and will briefly describe their function. Later chapters will cover in greater depth how to use the abstractions. Animation covers the topic of animation, and Evaluation and Constraint Solving discusses how to evaluate formulas using the API. In the following sections we will introduce the main abstractions that are available in ProB 2.0, that is, the model, state space and trace abstractions.
Experimenting with ProB 2.0
The best way to get a feel for ProB 2.0 is to try it out in a Groovy environment. Within the GUI, a Groovy shell can be opened from the Advanced menu.
ProB will automatically provide some predefined objects for interaction in Groovy shells. The most interesting predefined objects are stored in the api and animations variables.
The next section will only contain examples referencing the api variable, a singleton instance of the Api class, which has methods to load models for a number of different formalisms (currently classical B, Event-B, TLA+ and CSP). The animations variable is used to programatically interact with the user interface and will be referenced frequently in Animation.
Model Abstraction
The model abstraction provides static information about the current model that is being animated or checked. For Classical B and Event-B, this includes all of the information about the refinement chain and all of the different components (Machines, Contexts, Invariants, Variables, etc.). Currently, the model abstraction has been implemented for the Classical B, Event B, TLA+ and CSP-M formalisms. However, because we have implemented the abstraction with other formalisms in mind, it is not difficult to implement new formalisms.
A model is a graph whose vertices are components (e.g., machines and contexts) and whose edges are relations between components. The main differences between an Event-B model and its classical B counterpart are the artifacts and relationships they can contain. An Event-B Model consists of Machines and Contexts and the only relationships are refinement and sees while the classical B model contains machines, refinements and implementations and there are more relationships, for instance uses and includes.
All of the components in a model can be retrieved using the getComponents method. There is also a getComponent method to get a specific component by name. Because of some groovy features, these components can also be retrieved from the model by accessing the name of the component as if it were a field or property for the object.
| Please note, that it is not required to use Groovy, everything works from any JVM based language except for some syntactic sugar. |
The following example shows how to access a component with the Model API.
allComponents = model1.getComponents()
someComponent = model1.getComponent("the_machine")
sameComponent = model1.the_machine // works only in GroovyIn a similar way, it is possible to access the children components for a machine or context like the invariants or variables. When dealing with a B model, we can use the getInvariants method in a machine object to get a list of invariants defined in that machine. Invariants in classical B are automatically split into its conjuncts. We can also get a list of the events or a specific event using getEvents or getEvent("name"). From there we can get the list of guards [1] for an event. The following Groovy code shows an example that prints all events and their corresponding guard. We have recombined the guards into a single predicate.
machine.events.each {
event ->
guard = event.guard.join " ⋀ "
println "Event ${event.name}'s guard: ${guard}"
}The list of elements within a component is implemented with a special instance of list which also contains a mapping of the names of elements (if they have a name) so that specific elements can be retrieved from the list via name instead of iterating through the list and searching for the name. These elements can be accessed from the list via the getElement method. In a Groovy environment, these named elements also appear as fields on the class, which provides some nice syntactic sugar as seen in the following code snippet.
// get @grd1 from evt in Groovy environment
grd1 = model1.the_machine.events.evt.grd1
// equivalent call in Java syntax
grd1 = model1.getComponent("the_machine").getEvents().getElement("evt").getGuard("grd1")When we were implementing the API for the models, we took into account that classical B and Event-B specifications share many similarities. We wanted to be able to write scripts for both model objects without having to specify between the two. For this reason, there is also a mapping from a generic class (that is identical for both classical B and Event-B models) to the implementation specific elements.
For example, consider the similarities between classical B and Event-B. Both of the specifications have invariants (we break the classical B invariant down into its conjuncts). However, each of the Event-B invariants also a name. We therefore need two different implementations of the Invariant class, ClassicalBInvariant and EventBInvariant. Both the ClassicalBMachine and EventBMachine maintain a list of invariants, but there is also an implicit mapping from the Invariant class to the list of invariants which allows you to access the list via the getChildrenOfType method without knowing the type of the model in question. This is demonstrated in the following code examples
classicalBMachine.getChildrenOfType(Invariant.class)
eventBMachine.getChildrenOfType(Invariant.class)Because Groovy is dynamically typed, accessing the children elements in this way usually only makes sense in a Java environment.
Loading models into ProB
Now we need to load an actual specification file into ProB. This takes place in two steps: extracting the static information about the model into a Model object and then using that static information in order to load the model into the ProB CLI. In order to make the process as simple as possible, these two steps are separated. First, a ModelFactory is used to extract the Model represenation from a specification file. The Model representation then contains all of the information that it needs in order to load itself into ProB.
The ModelFactory is defined by the following interface:
public interface ModelFactory<T extends AbstractModel> {
public ExtractedModel<T> extract(String pathToSpecification);
}As you can see, a ModelFactory extracts a Model object from a given specification. From this interface we can also see that the statement made previously about the model’s ability to load itself into ProB is not completely accurate. A model contains several different components (for B these are machines or contexts). However, ProB requires one of these components to be specified as the so called main component, which is the component on which further animations will be based. The user will also likely want to set special preferences for a given animation, so this should also be available when loading the Model into ProB. For this reason, the loading function in an AbstractModel is defined as follows:
public abstract class AbstractModel extends AbstractElement {
public StateSpace load(AbstractElement mainComponent) {
load(mainComponent, Collections.emptyMap());
}
public abstract StateSpace load(AbstractElement mainComponent, Map<String,String> preferences);
}When extracting the model from a specification file, the main component is usually inherently specified. The user will extract the component /path/to/dir/spec1.mch and will expect that the component with the name spec1 will have been loaded. For this reason, we have introduced the ExtractedModel abstraction.
We have abstracted the loading mechanism for specifications so that it can be adapted to load any number of different formalisms. The classes responsible for loading the models basically have to perform three tasks: extract the static information about the specification in question, create a command to load the model into the Prolog kernel, and subscribe any formulas of interest (the subscription mechanism will be explained more in Evaluation and Constraint Solving. The load command consists of setting user specified preferences, a formalism specific load command for the model, and a request for ProB to start animating the model in question. Each formalism that is supported by ProB has its own factory responsible for loading it. These factories can be created via Dependency Injection, and they also have accessor methods in the Api class which makes it simple to load specifications in a groovy environment.
The load method of a factory takes three parameters:
* the String path to the specification file
* a Map<String,String> of user specified preferences (for list of possible preferences see the ProB wiki)
* a Groovy closure (the Groovy implementation of a lambda function) that takes the loaded model as a parameter and will execute user defined behavior
Load Function
As mentioned above, one of the parameters that is required by the model factory is a closure that performs user defined behavior after loading the model. For instance, the closure in the following listing would print the string representation of the model after loading it.
loadClosure = { model ->
println model
}Of course, this particular closure may not be useful for the user, but adding this functionality allows users to define actions that need to be taken directly after the model has been loaded. It is also possible to simply use an empty closure that does nothing. For those programming a Java environment, a predefined empty closure is defined as Api.EMPTY.
When loading the model into the user interface, we want formulas of interest to tell the state space to evaluate themselves in every step of the animation so that their values can be cached and easily retrieved. This evaluation mechanism is described further in Evaluation and Constraint Solving. To do this, we have implemented the Api.DEFAULT closure which will tell ProB that all invariants, variables, and constants are of interest.
As mentioned before, the model factories (ClassicalBFactory, EventBFactory, CSPFactory, and TLAFactory) can be retrieved from the injector framework. However, there are also methods for loading the specifications in the Api class to allow access from a Groovy environment. The next sections will briefly cover how to load different specifications and the special characteristics for the specification in question. Each of the load methods in the Api take three parameters, but there are also default values for the parameters that are supplied if the user does not choose to define one of them. To take the optional parameters into account, groovy compiles a single method call into three separate method calls as shown in the following:
// The following calls have identical results
m = api.formalism_load("/path/to/formalism/formalism.extension")
m = api.formalism_load("/path/to/formalism/formalism.extension", Collections.emptyMap())
m = api.formalism_load("/path/to/formalism/formalism.extension", Collections.emptyMap(), api.getSubscribeClosure())As you can see from the third call, the load closure in api.formalism_load will be set to api.getSubscribeClosure() if not defined by the user. What does this method do? As stated in the above sections, there are two default load closures contained in the Api class (Api.DEFAULT and Api.EMPTY). If the user does not want to subscribe all formulas of interest by default, they can manipulate this via the boolean flag api.loadVariablesByDefault
api.loadVariablesByDefault = true // register all formulas of interest
api.getSubscribeClosure() == api.DEFAULT // true
api.loadVariablesByDefault = false // do not register any formulas
api.getSubscribeClosure() == api.EMPTY // true
// It is also possible to create new DEFAULT behavior
olddefault = api.DEFAULT
api.DEFAULT = { model ->
// This closure subscribes variables from the highest refinement
model.getMainComponent().variables.each {
it.subscribe(model.getStateSpace())
}
}
api.loadVariablesByDefault = true
api.getSubscribeClosure() != olddefault // true
api.getSubscribeClosure() == api.DEFAULT // trueLoading Classical B Specifications
The following listing shows how classical B specifications are loaded.
model1 = api.b_load("/path/classicalb/machine.mch")
model2 = api.b_load("/path/classicalb/refinement.ref")
// load with preference COMPRESSION set to true
model3 = api.b_load("/path/classicalb/machine.mch", [COMPRESSION : "true"])
// loading from the ClassicalBFactory itself
classicalBFactory.load("/path/classicalb/machine.mch", Collections.emptyMap(), api.getSubscribeClosure())Loading Event-B specifications
Loading Event-B specifications is possible via the api.load_eventb method. However, there are several different ways to serialize Event-B models, so there are also more ways to load an Event-B specification. The easiest way is to load an Event-B specification from the static checked files produced by Rodin:
model1 = api.eventb_load("/path/eventb/machine.bcm")
model2 = api.eventb_load("/path/eventb/context.bcc")
// Loading from the EventBFactory itself
eventBFactory.load("/path/eventb/machine.bcm", Collections.emptyMap(), api.getSubscribeClosure())If a user attempts to load an unchecked file (.bum or .buc), the loading mechanism attempts to find the correct corresponding checked file.
However, the tool also supports two further formats for loading an Event-B model. The first is the .eventb format, which is the format exported from Rodin for the Tcl/Tk version of ProB. Unfortunately, when loading from this format, it is not possible to find any static information about the model, so the model object that is constructed will be empty.
// the following calls are equivalent
api.eventb_load("/path/eventb/machine_mch.eventb")
eventBFactory.loadModelFromEventBFile("/path/eventb/machine_mch.eventb", Collections.emptyMap(), api.getSubscribeClosure())Rodin allows users to export projects in the .zip format, so we also support the loading of Event-B specifications directly from the zipped file. Here we need further information: the name of the particular component that the user is interested in. As with the other load methods, there are optional parameters that may be specified
// searches recursively until machine.bcm is found
model1 = api.eventb_load("/path/eventb/model.zip", "machine")
// searches recursively until context.bcc is found
model2 = api.eventb_load("/path/eventb/model.zip", "context")
// loading a zip file from EventBFactory itself
eventBFactory.loadModelFromZip("/path/eventb/model.zip", "machine", Collections.emptyMap(), api.getSubscribeClosure()))Loading TLA+ specifications
ProB provides support for TLA+ specifications via a translation tool developed separately to translate TLA+ specifcations into the AST format used by the classical B parser [1]. Using the same mechanism, we translate the TLA+ mechanism into a ClassicalBModel during loading, so the ProB API handles TLA+ models exactly the same way it treats classical B specifications. The load command can be seen in the following code snippet. What is worth noting here is that the model object returned from the load command is for all intents and purposes to the API actually a ClassicalB model due to the translation process.
// As with classical B and Event-B, the following calls are equivalent
api.tla_load("/path/tla/specification.tla")
tlaFactory.load("/path/tla/specification.tla", Collections.emptyMap(), api.getSubscribeClosure())Loading CSP-M Specifications
The CSP-M specifications are parsed using an external library.
We currently don’t have a way to extract static data structures from CSP specifications, so the CSPModel that is created by loading the specification is empty. For this reason also, the default load closure for CSP-M specifications is Api.EMPTY. The different ways to load CSP specifications can be seen in the following
// The following calls are equivalent
api.csp_load("/path/csp/specification.csp")
cspFactory.load("/path/csp/specification.csp"), Collections.emptyMap(), api.EMPTY)State Space
While the model describes the static properties of a development, the StateSpace describes the dynamic properties. There is a one-to-one relationship between a StateSpace and a model. The StateSpace is the corresponding label transition system for a particular model that is calculated by ProB.
The state space represents the whole currently known world for an animation. It is lazily explored, i.e., when we access a state within the StateSpace, ProB will fetch the information from Prolog automatically and transparently. The only observation that can be made is that the fetching of some states takes longer than the ones that are already cached in the StateSpace.
The class itself is based on an LRU cache implementation. Because the states are all cached within the Prolog binary, we do not want to cache all of them on the Java side in order to ensure that the memory footprint of the Java API remains reasonably small. The cache currently stores up to 100 states, although we may make this customizable in the future.
On the Prolog side, the States are identified by a unique String identifier (which is currently implemented with a counter that increments every time a state is discovered). For this reason, the states can be retrieved from the StateSpace via the getState method. If a state has been cached for the specified identifier, this is retrieved from the Java cache. Otherwise, the Prolog kernel is queried to see if the specified identifier maps to an valid state in the state space, and if so, the state is constructed, cached, and returned to the user.
The StateSpace is also used as the gateway to the Prolog binary. It implements the IAnimator interface and therefore we can submit commands using the state space.
The state space that corresponds to a loaded model can be obtained using the model’s getStateSpace() method. We can also use Groovy’s special syntax for type coercion:
sspace = model1.getStateSpace()
sspace = model1 as StateSpaceState
As stated before, the state space is the labeled transition system for a model. The state space maintains a cache of states that have been accessed from within the state space. These states are represented by object of class State, and the relationship between the states is specified using objects of class Transition. The Transition objects are not explicitly saved in the state space, but the graph maintains its structure because each state maintains a list of outgoing transitions from itself. The transitions are not saved by default, rather are calculated lazily when they are needed. The outgoing transitions from a given state can be calculated via the explore method, which also retrieves other information from the Prolog kernel including if the invariant is broken and the calculated values of the formulas of interest. The following listing shows how to explore a state (thereby calculating outgoing transitions). There is also a getOutTransitions method which performs both of these steps at once.
// Code snippet 1:
x = sspace.getRoot() // retrieves root state.
x.getTransitions().size() == 0 // true, when the state is not explored
x.explore()
x.getTransitions().size() != 0 // true, when ProB has calculated a transition
// Code snippet 2:
x = sspace.getRoot()
x.getOutTransitions().size() != 0 // getOutTransitions explores the state if
// necessary, returning the resulting transitionsIt is also possible to use the state object for evaluation of formulas and for animation, but these functionalities will be explained in detail in the next chapters.
Transition
As explained in the last section, a state maintains a list of all outgoing transitions. But what do these transitions contain? The transitions represents the instantiation of an event from one state into another. The transition object contains the unique identifier that ProB assigns to the transition, the name of the event that is initiated, the source state and destination state for the transition, and the values of the parameters and return values that ProB has calculated. The following code snippet shows the basic API for a transition object. The getRep method is also available which creates a pretty representation of the transition based on the syntax of the model that is being animated.
transition = sspace.getRoot().getOutTransitions().first()
transition.getSource() == sspace.getRoot() // will be true
destination = transition.getDestination()
transitionId = transition.getId()
params = transition.getParams()
returnVs = transition.getReturnValues()
println transition.getRep() // pretty print of the transitionWhen using transitions, however, it is important to be aware that not all of these fields are filled by default. The source and destination states, the id, and the name are all defined, but the parameters and return values are retrieved lazily only if they are needed. This is because many specifications written in classical B or Event-B have very large parameter values, and these parameter values need to be sent from the prolog side to the Java side. Because the communication between the two uses sockets and the parsing of strings, having to send large strings results in a visible performance decrease. Often, the user doesn’t need to use the parameter values, so it made sense to retrieve them lazily from Prolog.
However, even retrieving the parameters and return values at a later time can be inefficient if you are dealing with multiple transitions for which you need to retrieve the parameters at the same time. For this reason, we have made the evaluateTransitions method in the state space, which takes a collection of transitions and retrieves their parameters and return values in one go by composing the requests to Prolog into one query as described in Low Level API. This results in better performance because for a list of transitions with n elements, only one communication step is required instead of n steps.
In addition to the evaluateTransition method, we have also modified the getter methods for classes containing lists of transitions (i.e. the getOutTransitions method in the State class and the getTransitionList and getNextTransitions method in the Trace class). S
stateSpace.evaluateTransitions(list_of_transitions)
state.getOutTransitions() == state.getOutTransitions(false)
state.getOutTransitions(true) // all transitions will be evaluated
trace.getTransitionList() == trace.getTransitionList(false)
trace.getTransitionList(true) // all transitions will be evaluated
trace.getNextTransitions() == trace.getNextTransitions(false)
trace.getNextTransitions(true) // all transitions will be evaluatedThe Trace class is explained in further detail in the next section. These getter methods take an additional parameter evaluate (which is by default set to false), and if set to true, will evaluate all of the transitions at once.
Trace
For some tools, the StateSpace abstraction may be sufficient. But when it comes to animation and the concept of a current state, a further abstraction, called a Trace, becomes handy. Without the trace abstraction each tool would have to explicitly store the lists of states that has been executed.
A trace consists of a linked list of states which correspond to a path through the state space. There is also a pointer in the list which identifies the current state.
If we go back in time, the trace keeps future states. If we change a decision in the past, the trace drops the future. It behaves in the same way your browser history does.
One instance of Trace corresponds to exactly one trace within the animation. Each trace is associated with exactly one state space, but we can have many different traces on top of a single state space.
The Trace objects are immutable. This means that whenever an animation step is performed (forward, backward, or simply adding a transition to the trace) a new Trace is returned. We use structural sharing to efficiently implement the operations. We do not require copying the list each time we change something.
There can be an arbitrary number of Trace objects for any given instance of a state space. A trace is created from one specified start state. It can also be created from the state space object itself, at which point it is assumed that the start state is the root state
t = new Trace(someStateSpace)
t2 = new Trace(someStateSpace.getRoot())
// t and t2 are equivalent
// anyEvent randomly follows a transition
arbitraryState = stateSpace.getRoot().anyEvent().anyEvent()
t = new Trace(arbitraryState) // start from arbitrary stateTraces are implemented as two "pointers" into an immutable linked list. This allows us to always create new Trace objects while still being efficient.
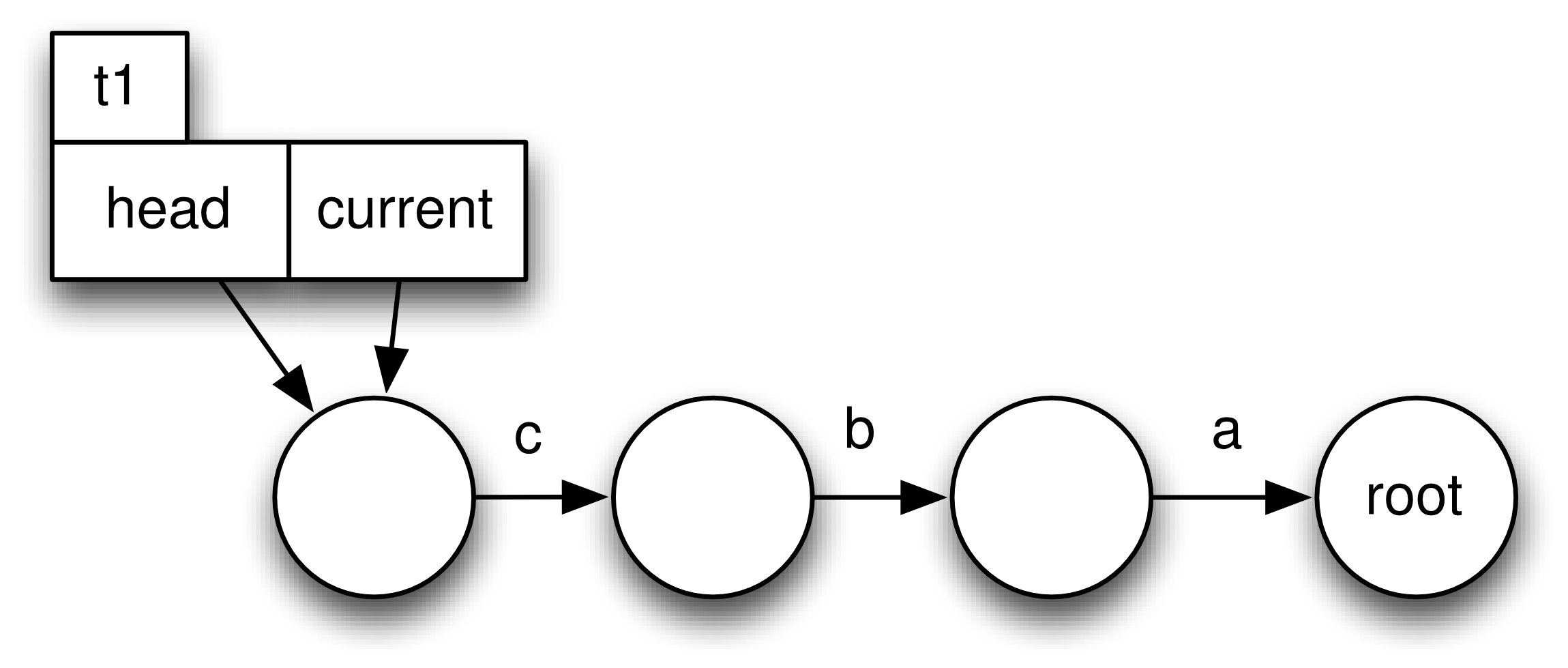
The following code demonstrates how traces evolve:
t1 = randomTrace(new Trace(),3);
t2 = t1.back()
t3 = t2.anyEvent("d")Initially we create a random Trace t1 of length 4 (Figure 2). Let’s say the Trace consists of the events a,b, and c. Then we call the back method on t1 yielding a new Trace object t2 (Figure 3). Finally we execute some event d. In Figure~\ref{fig:trace_evolve} we show the case where t1.getCurrentState() yields a different state than t3.getCurrentState(). Otherwise t3 would be a copy of t1.
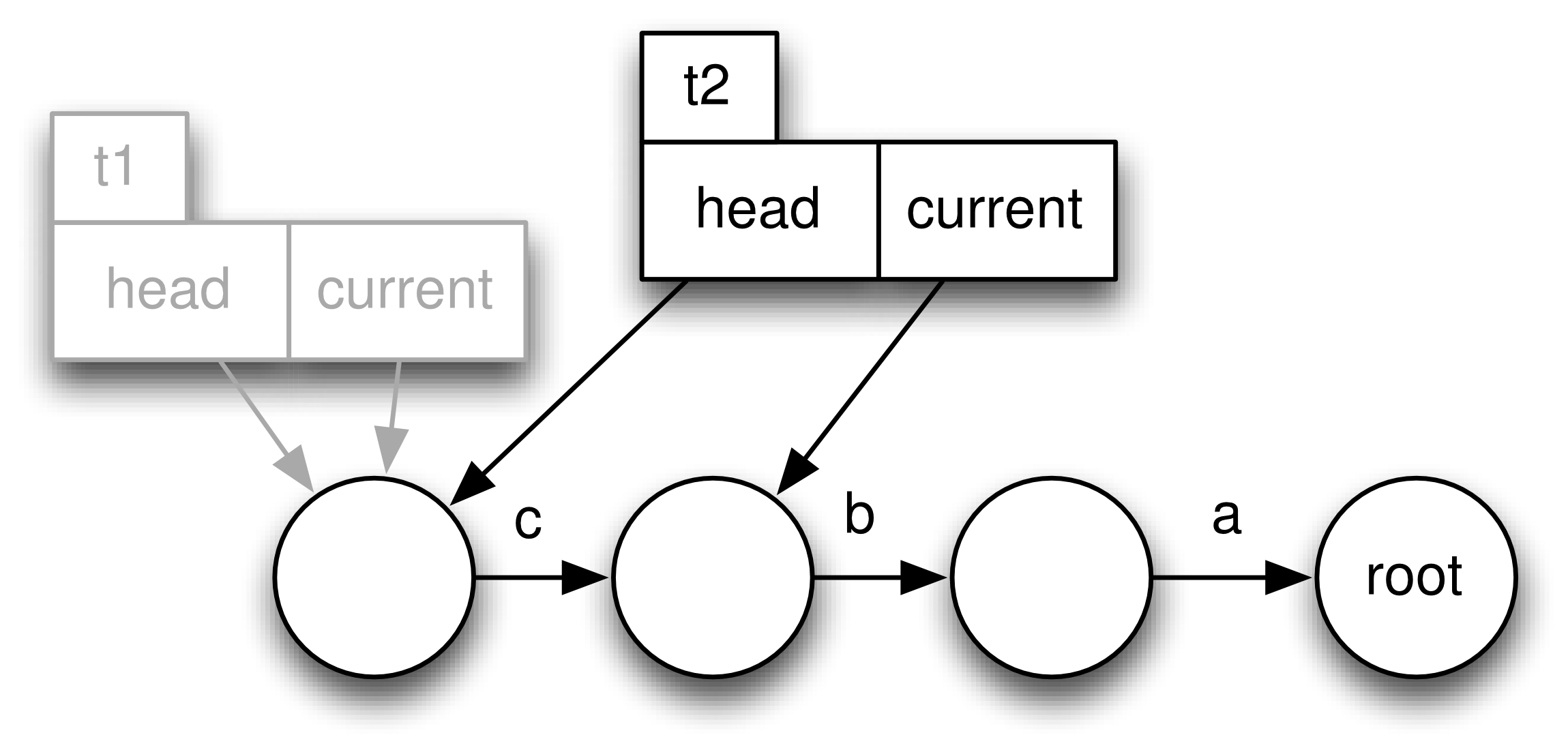
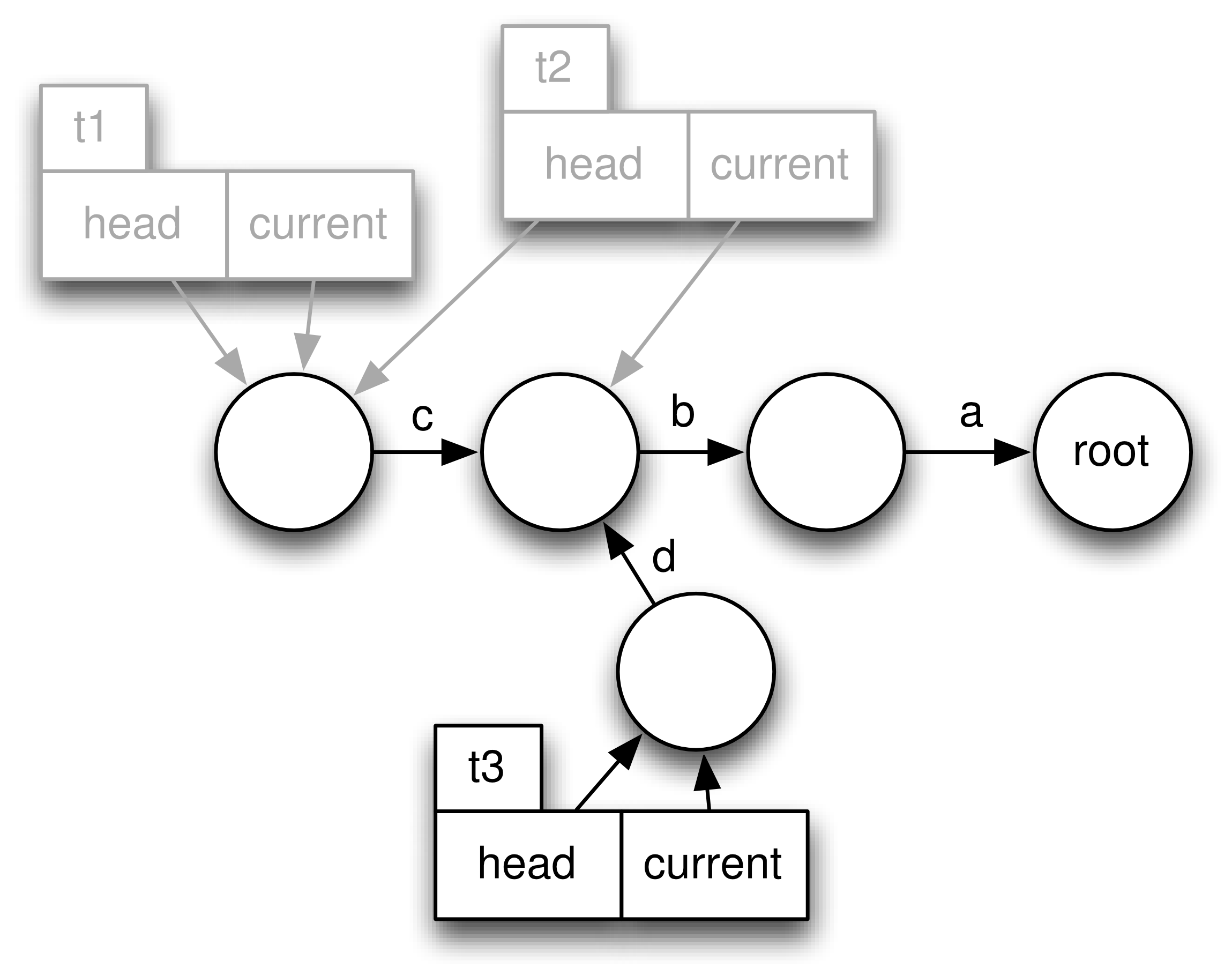
Note, that almost all elements are shared between the Traces, we do not have to copy the List in order to have immutable values, so the implementation is efficient.
Animation
It is possible for the user to perform animation manually using the state and transition abstractions, or to use the trace abstraction which allows the user access to previously executed transitions, and the ability to move within the trace. This chapter will describe in detail all of the different ways that it is possible to perform animation using the provided abstractions.
Animation via State
We can also use a state to start animating the model. For instance, we can "execute" an event, resulting in the successor state by executing the anyEvent method of the state instance. There is also a method anyOperation which is just a synonym for anyEvent. The anyEvent Method can be used to construct random traces.
y = x.anyEvent()
y = x.anyOperation()
// create random walks
def random_trace(sspace) {
def t = [sspace.root]
100.times { t << t.last().anyEvent() }
return t;
}Another thing we typically want to do is to execute a specific event using the perform method of the state object. At this point you need to chose an event that you want to execute. It has to be enabled in the state, but you can provide additional guards to restrict the parameters. For instance if the event foo is enabled and we want call it with the parameter x set to the value 42, we can use the perform method:
y = x.perform("foo",["x=42"])The second argument is a list of predicates that are added to the guard of the event. They are used to further restrict the parameters. In our case foo could have been defined as
foo = ANY x WHERE x : NAT THEN y := y + x ENDIf we execute the event using anyEvent and ProB is allowed to choose any natural number, typically it chooses 0. Adding x=42 as an additional predicate will force ProB to set x to 42. Note that any predicate is allowed, we could also use for instance x:42..47 which allows ProB to choose any number between 42 and 47.
The name of the formal parameters can only be retrieved indirectly from the machine. We can now implement a new execution method that does use positional arguments instead of named arguments using B predicates.
fp = mch.getEvent(o.getName()).getParameters()
def execute(machine, state, operation_name, Object... params) {
formal_params = machine.getEvent(operation_name).getParameters()
pred = [formal_params,params]
.transpose()
.collect { a,b -> a.toString() + "=" + b.toString() }
x.perform(name,pred)
}A call would look like execute(mch, x,"foo", 42) or for an operation with three parameters it would look like execute(mch,"bar",1,"{}",-3).
Animation via Trace
The Trace class is the main abstraction intended for animation. This section explains how to use the trace API. We can use the trace to track a succession of states. Traces also support the anyEvent method.
t2 = t.anyEvent() // extend the trace by one random state
def randomTrace(t,n) {
def result = t
n.times { result = result.anyEvent() }
result // return value
}
t3 = randomTrace(t2,100)
t4 = t3.anyEvent("foo") // execute foo
t5 = t4.anyEvent(["foo","bar"]) // execute either foo or bar
t6 = t5.anyOperation() // synonym for anyEventA Trace has a current state, typically the last state in the trace. but we can "go back in time". This changes the current trace to some other state contained in the trace.
t = randomTrace(new Trace(sspace),100) // a rather long trace
t.getCurrentState()
t.canGoForward() // false
t.canGoBack() // true
t = t.back()
t.canGoForward() // true
t = t.forward()
t.canGoForward() // falseSynchronized Animations
When dealing with model composition/decomposition there is interest in synchronized animations. This is usually the case when a model has been decomposed into separate components. It is of course possible to animate the components separately by creating a Trace object for each separate component. However, often a user wants to create a composed animation in which multiple Trace objects can be animated at once. In such an animation, specific events from different Traces can be selected and synchronized. Here, synchronized means that when an event from one trace is fired, events that are synchronized will attempt to trigger as well. If one of the triggered events fails, the whole animation step fails.
A synchronized trace object, or SyncedTrace, can be created by specifying a list of Traces and a list of SyncedEvents. These SyncedEvents are defined by the user and encapsule name and parameter combinations from different traces that are then coupled under a user defined event name.
// t0, t1, t2 are Trace objects
tt = new SyncedTraces([t0,t1,t2], [
new SyncedEvent("sync1").sync(t0,"foo",["x < 5"]).sync(t1,"bar",[]),
new SyncedEvent("sync2").sync(t2,"baz",[]).sync(t0,"foo",["x > 5"]),
])Once a SyncedEvent has been defined for a SyncedTrace, this event can be executed on the class which results in the previously defined events being fired in the underlying Trace objects.
tt1 = tt.sync1() // The Java equivalent of this call is tt.execute("sync1")
assert tt1.traces[0].getCurrentTransition().getName() == "foo"
assert tt1.traces[1].getCurrentTransition().getName() == "bar"
assert tt1.traces[2] == t2
tt2 = tt.sync2()
assert tt2.traces[0].getCurrentTransition().getName() == "foo"
assert tt2.traces[1] == t1
assert tt2.traces[2].getCurrentTransition().getName() == "baz"If the user wants to execute an event on one of the internal traces, the execute method allows this Trace object to be specified via index.
tt3 = tt.execute(1, "moo", ["pp : {1,2,3}"])
assert tt3.traces[0] == t0
assert tt3.traces[1].getCurrentTransition().getName() == "moo"
assert tt2.traces[2] == t2However, when executing if the event that is triggered is one of the synced events, triggering this animation step will trigger the synced events in the other Trace objects as well.
tt4 = tt.execute(0, "foo", ["x < 5"])
assert tt4.traces[0].getCurrentTransition().getName() == "foo"
assert tt4.traces[1].getCurrentTransition().getName() == "bar"
assert tt4.traces[2] == t2
tt5 = tt.execute(1, "bar", [])
assert tt5.traces[0].getCurrentTransition().getName() == "foo"
assert tt5.traces[1].getCurrentTransition().getName() == "bar"
assert tt5.traces[2] == t2
tt6 = tt.execute(0, "foo", ["x > 5"])
assert tt6.traces[0].getCurrentTransition().getName() == "foo"
assert tt6.traces[1] == t1
assert tt6.traces[2].getCurrentTransition().getName() == "baz"
tt7 = tt.execute(2, "baz", [])
assert tt7.traces[0].getCurrentTransition().getName() == "foo"
assert tt7.traces[1] == t1
assert tt7.traces[2].getCurrentTransition().getName() == "baz"Triggering an event whose name and parameter combinations do not exactly match those defined in the synced event will not trigger any synced event.
tt8 = tt.execute(2, "foo", ["x = 5"])
assert tt8.traces[0].getCurrentTransition().getName() == "foo"
assert tt8.traces[1] == t1
assert tt8.traces[2] == t2If any animation step in any of the underlying Trace classes fails, the entire animation will also fail. In this example, attempting to execute the synced event sync1 while either traces[0].foo("x <5") or traces[1].bar() is not enabled will result in an exception.
Evaluation and Constraint Solving
This chapter will demonstrate how we evaluate formulas in the context of a formal model. It also demonstrates how we can use ProB’s constraint solver.
Evaluation
Several classes offer an eval method, the result depends on the specific class. We have already seen how we can evaluate an expression or prediacte in a state to retrieve state values. But we are not limited to variables, we can actually ask for any expression. Say in a state x the value of a is 7 and the value of b is 5. We can then ask ProB for the value of the expression a + b.
x.eval("a + b") // returns 12 if a=7 and b=5 in state x
x.eval("a < b") // returns FALSE
x.eval("#z.z<a & z<b") // returns TRUE (z=6)The input of eval is either an instance of IEvalElement or a String. If the input is a String, it will be parsed with the same formalism as the model. This means, if we are in the context of a classical B model, strings are treated as classical B formulas, if we are in the context of an EventB model a string is parsed as Event-B, etc.
If we plan to submit the same formula more than once, we should consider turning it into an instance of IEvalElement because this saves parsing the string multiple times. Each formalism has its own implementation of the IEvalElement interface. Once a string has been turned into an IEvalElement, it can be evaluated in any formalism.
\\ classicalb_x is a classical B state
\\ eventb_x is an Event B state
classical_b.eval("2**4") // 16
eventb_x.eval("2**4") // Type Error
cb_eval_element = new ClassicalB("2**4")
classical_b.eval(cb_eval_element) // 16
eventb_x.eval(cb_eval_element) // 16
eventb_x.eval("2**4" as ClassicalB) // 16
eventb_x.eval(new ClassicalB("2**4")) // 16Trace also implements eval, but instead of evaluating the expression or predicate in a single state, it will evaluate it for the whole trace, i.e., it will return a list of results. The results are tuples containing the state ID and the result. In addition to the eval method a trace also has a method evalCurrent(), which evaluates a formula in the current state of the trace.
The StateSpace class is responsible for actual evaluation, it provides an eval method that takes two arguments, a state Id and a list of IEvalElements. It returns a corresponding list of EvalResult objects.
This means, that we can evaluate multiple expressions and predicates in one go. This is important to avoid communication overhead with Prolog.
Note that there is no eval method that takes a single formula and evaluates the formula for every known state. We decided that using the same name for a method with that semantics would be too dangerous if we call it accidentally on a big state space. However, there is a method evaluateForEveryState, which actually evaluates a formula in every known state. There is also a method evaluateForGivenStates that takes a list of state IDs and a list of IEvalElements and evaluates each formula for each state.
As mentioned, the result of evaluation is an instance of the EvalResult class.
r = x.eval("base**4") // x is some state id, base is a B variable
r.getClass() // class de.prob.animator.domainobjects.EvalResult
r.getValue() // if in state x the value of base is 2
// then we get "16" (as a String)Note that we could also evaluate predicates, e.g., base < 3.
Constraint Solving
Constraint solving is very similar to evaluation, the difference is that constraint solving only uses types from a model, but not an actual state. For example, we could ask which value b should have to satisfy the equation b * 4 = 16 or we could ask for the set of all possible values of b {b | b * 4 = 16}, which will return {-4,4}.
The constraint based solver can be controlled through the CbcSolveCommand. It is very similar to evaluation. In fact, eval will also try to find a solution for free variables.
r = x.eval("b**4 = 16") // x is some state id, b is a fresh variable
r.getValue() // "TRUE"
r.getSolutions() // A hashmap containing variable-value bindings
r.getSolutions().get("b") // "-2"We can also solve formulas with multiple variables and we can translate results to a unicode representation.
r = x.eval("{a,b|a < 100 & b:NAT & a>b & b ** 4 = a}")
r.getValue() // {(16|->2),(81|->3)}
de.prob.unicode.UnicodeTranslator.toUnicode(r.getValue()) // {(16↦2),(81↦3)}However evaluation is only applicable in the context of a state. If we want to solve constraints outside of a state, we have to use CbcSolveCommand.
f = "{a,b|a < 100 & b:NAT & a>b & b ** 4 = a}" as EventB
c = new CbcSolveCommand(f)
sspace.execute(c)
c.getResult()Of course we can introduce some syntactic sugar
def solve(model, fstring) {
f = model.parseFormula(fstring) // use correct formalism
c = new CbcSolveCommand(f)
model.getStateSpace().execute(c)
c.getResult()
}Note that Groovy can be very helpful to create small domain specific languages. For example we can create a small DSL to manipulate predicates.
String.metaClass.and = {b -> "("+delegate+") & ("+b + ")" }
not = { "not("+it+")" }
String.metaClass.implies = {b -> "("+delegate +") => (" + b + ") "}
ArrayList.metaClass.conj = { delegate.collect{it.toString()}.inject {a,b -> a & b} }The first line changes the behavior of the & operator for strings. The second line introduces a negation. The third line introduces an implies method to the String class. Finally we add a join method to the ArrayList class allowing us to turn a list of predicates into a conjunction.
a = "x < 9"
b = "2 = y"
a & b // result is "(x < 9) & (2 = y)"
not(a & b) // result is "not((x < 9) & (2 = y))"
a.implies b // result is "(x < 9) => (2 = y)"
["x = 1","y = 2","x < y"].join() // result is "((x = 1) & (y = 2)) & (x < y)"The constraint solver is a versatile tool that can be used in many situations, for instance, we could use it to identify events that are dead. A dead event find out if the guard G of an event contradicts the invariant J, i.e., there is a solution for J ➝ ¬G.
def dead_event(model, component, name) {
def invariant = model.getComponent(component).getInvariant().conj()
def guard = model.getComponent(component).getEvent("name").guards.conj()
def predicate = invariant.implies(not(guard));
solve(model,predicate)
}Dependency Injection
We have decided to use the Guice framework for dependency injection. Although this is just an implementation detail it is important to get a basic understanding of how it works and why we use it in order to build tools on top of ProB 2.0. A more complete introduction to dependency injection and the Guice framework can be found in [2] and the Guice website.
Dependency injection is used when we create an instance of a class. As an example, we will use the Api class. The class depends on a class that constructs factories which construct model objects from files. It also depends on a provider that can create instances of IAnimator, which coordinates the execution of commands.
There are several possible ways to setup the dependencies. We could just create the dependency inside the constructor
public Api() {
this.modelFactoryProvider = new FactoryProvider();
this.animatorProvider = new AnimatorProvider();
}But unfortunately the FactoryProvider requires four concrete Factory classes, ClassicalBFactory, CSPFactory, EventBFactory and TLAFactory. This would lead to a very intertwined code. Also it would become very hard to test the code in isolation.
A better way would be to pass in the dependencies of a class as parameters of the constructor
public Api(FactoryProvider modelFactoryProvider, Provider<IAnimator> animatorProvider) {
this.animatorProvider = animatorProvider;
this.modelFactoryProvider = modelFactoryProvider;
}Now we moved the burden of creating the dependencies to the code that calls the constructor. This is very useful in a test, where we can now pass whatever we want when we setup the object. For instance, if we want to test the interaction of the Api with the animator provider, we could just use null as the modelFactoryProvider and a mock object as the animatorProvider. This mock object could simulate the real provider without actually starting up probcli.
But we only moved the problem one level up. However, the class that requires Api simply does the same thing. Its constructor takes an Api instance as a parameter.
If done by hand this approach would lead to a very complicated top level object, where we construct all the objects and then create a potentially complex object graph.
This is where dependency injection frameworks like Guice or Spring come into play. We annotate the constructor with @Inject and leave object instantiation to Guice.
@Inject
public Api(final FactoryProvider modelFactoryProvider, final Provider<IAnimator> animatorProvider) {
this.animatorProvider = animatorProvider;
this.modelFactoryProvider = modelFactoryProvider;
}We can still manually construct the object for testing purposes, but in the actual application, instead of calling new, we use a so called Injector. If we ask the Injector to construct an Object, it will automatically setup all dependencies. The injector is configured using so called modules.
If you build tools on top of ProB 2.0 you will likely require some of ProB’s objects, so you have to interact with Guice to get proper objects.
| Never create ProB objects whose constructor is annotated with @Inject by calling new unless you are writing a test. |
The correct way is to get the injector and ask it for an instance. The de.prob.Main class contains the application injector. So if you want to get an instance of the Api class you would do it like this:
Api api = Main.getInjector().getInstance(Api.class);If you want to use Guice in your own tool, you can create an Injector and tell ProB to use it.
Module myModule = new MyModule();
Injector myInjector = Guice.createInjector(Stage.PRODUCTION, mymodule, new MainModule());
Main.setInjector(myInjector);MainModule is ProB’s default module. It is a composition of other modules. If you want to use ProB as it is, you typically use MainModule. But you can change parts of ProB by exchanging ProB’s modules with your own configuration. For instance, you could configure the injector to use your own implementation of the Api class instead of ProB’s version.
Program Synthesis
Program synthesis is the task of generating executable programs from a given specification usually considering a domain specific language. There are many ways to specify the behavior of a program to be synthesized like logical or mathematical formulae (e.g., in the form of pre- and post-conditions) or explicit input-output examples. The ProB Prolog core provides an implementation to synthesize B predicates or complete machine operations from explicit state input-output examples. The ProB2 Java API provides an interface to utilize the program synthesis backend. The implemented synthesis technique is based on the work by Susmit Jha, Sumit Gulwani et al. [https://people.eecs.berkeley.edu/~sseshia/pubdir/icse10-TR.pdf] A synthesis task is encoded as a constraint satisfaction problem in B using the ProB constraint solver and its available backends to find valid solutions.
In order to use the synthesis backend we expect the B machine to be loaded for which B code should be synthesized. The input-output examples describing the behavior of a program to be synthesized then refer to a subset of machine variables. In particular, synthesis expects a set of positive and negative examples. In case of synthesizing a B predicate, the synthesized predicate is true for the positive examples and false for the negative examples. Here, an example is a single machine state (input). In case of synthesizing a B machine operation, the positive examples are used to synthesize the B operation’s substitution while both sets of examples are used to synthesize an appropriate precondition for the operation if necessary. Here, an example consists of inputs and outputs, i.e., before- and after-states.
The main class is BSynthesizer which expects the statespace of a currently loaded B machine on construction:
BSynthesizer synthesizer = new BSynthesizer(stateSpace);Using input-output examples to specify the behavior of a program is most comfortable for the user but most difficult for program synthesis itself. As input-output examples possibly describe ambiguous behavior we provide two modes for synthesis: * FIRST_SOLUTION: Return the first solution found. * INTERACTIVE: Search for another non-equivalent program after finding a solution. There are three possible outcomes: * If the constraint solver finds a contradiction, we have found a unique solution and return the program synthesized so far. * If the constraint solver cannot find a solution because of exceeding the solver timeout, we return the program synthesized so far. On the one hand, this program might not be the one expected by the user if the examples describe ambiguous behavior. On the other hand, a synthesized program does always satisfy the provided examples. Thus, in practice, completeness depends on the selected solver timeout. * If we find another non-equivalent program, we search for an example distinguishing both programs referred to as a distinguishing example. That is, an input state for which both programs yield different outputs. This example can be validated by the user and be considered in the set of examples for another run of synthesis possibly guiding synthesis to a unique solution. For instance, assume we want to synthesize a B predicate by providing a set of positive and negative examples and synthesis has found the predicate "x > 0" first. Assuming the examples describe ambiguous behavior synthesis may find another non-equivalent predicate "x > 1". A distinguishing example would then be "x = 1" as the first predicate is true and the second one is false for this input. The synthesis mode can be set using the method setSynthesisMode():
synthesizer.setSynthesisMode(SynthesisMode.INTERACTIVE);We provide three classes to create examples: * VariableExample.java: An example for a single machine variable consisting of the machine variable’s name and its pretty printed B value. * Example.java: An example for a machine state which is described by a set of variable examples. * IOExample.java: An input-output example which is described by two examples for input and output respectively.
As mentioned above one can either synthesize a B predicate or a complete machine operation. To do so, a BSynthesizer object provides two methods synthesizePredicate() and synthesizeOperation().
Synthesizing a B predicate expects a set of positive examples and a set of negative examples. For instance, assume we have loaded a machine that has an integer variable called "floor" and want to synthesize the predicate "floor > 0". First, we create the set of positive and negative examples:
HashSet<Example> positiveExamples = new HashSet<>();
positiveExamples.add(new Example().addf(new VariableExample("floor", "1")));
positiveExamples.add(new Example().addf(new VariableExample("floor", "2")));
positiveExamples.add(new Example().addf(new VariableExample("floor", "3")));
HashSet<Example> negativeExamples = new HashSet<>();
negativeExamples.add(new Example().addf(new VariableExample("floor", "0")));
negativeExamples.add(new Example().addf(new VariableExample("floor", "-1")));
negativeExamples.add(new Example().addf(new VariableExample("floor", "-2")));Note, the method addf() is just a wrapper for a Java set’s add() method enabling a functional style. Afterwards, we are able to run synthesis using synthesizePredicate():
try {
BSynthesisResult solution = synthesizer.synthesizePredicate(positiveExamples, negativeExamples);
if (solution.isProgram()) {
SynthesizedProgram synthesizedProgram = (SynthesizedProgram) solution;
System.out.println("Predicate: " + synthesizedProgram);
}
} catch (BSynthesisException e) {
//
}A BSynthesisResult is either a program or a distinguishing example depending on the selected synthesis mode. If synthesis fails, an exception is thrown providing an appropriate error message.
Now assume that we want to synthesize a B machine operation that increases the variable "floor" by one. Again, we first create the set of positive and negative examples which are now examples for input and output:
positiveIOExamples.add(new IOExample(
new Example().addf(new VariableExample("floor", "0")),
new Example().addf(new VariableExample("floor", "1"))));
positiveIOExamples.add(new IOExample(
new Example().addf(new VariableExample("floor", "1")),
new Example().addf(new VariableExample("floor", "2"))));
positiveIOExamples.add(new IOExample(
new Example().addf(new VariableExample("floor", "2")),
new Example().addf(new VariableExample("floor", "3"))));Afterwards, we are able to run synthesis:
try {
BSynthesisResult solution =
bSynthesizer.synthesizeOperation(positiveIOExamples, new HashSet<>(), lib);
if (solution.isProgram()) {
SynthesizedProgram synthesizedProgram = (SynthesizedProgram) solution;
System.out.println("Operation: " + synthesizedProgram);
}
} catch (BSynthesisException e) {
//
}Note, we do not provide any negative examples but pass an empty set. If we would provide negative input-output examples, an appropriate precondition would be synthesized for the machine operation. That is, the synthesized operation is enabled for the inputs of the positive examples and disabled for the inputs of the negative examples.
The employed synthesis technique is based on the combination of program components and, thus, requires a predefined set of library components. For instance, an integer addition is such a library component. If using synthesis as described above, a default library configuration is used. This default configuration tries to use as little components as possible and successively intermingles components or increases the amount of specific components if no solution can be found using the current library configuration. As this default library configuration is mainly selected randomly, synthesis possibly lacks for performance compared to using the exact library of components that is necessary to synthesize a program. To that effect, the user is also able to specify the exact library configuration to be considered during synthesis. We provide the class BLibrary to create a specific library configuration.
The enum LibraryComponentName provides all B components that are supported by the synthesis backend. Constructing a BLibrary object provides an empty library considerings the default configuration. We thus have to state that we want to use a specific library of components only and add the desired components using their names. For instance, we want to create a component library using an integer addition and subtraction:
BLibrary lib = new BLibrary();
lib.setUseDefaultLibrary(false);
lib.addLibraryComponent(LibraryComponentName.ADD);
lib.addLibraryComponent(LibraryComponentName.MINUS);A BLibrary object can be passed as the third argument for synthesizePredicate() and synthesizeOperation() respectively.
The employed synthesis technique is based on constraint solving and, thus, each component has a unique output within a synthesized program. For instance, to synthesize the predicate "x + y + z > 2" we need two addition components. There are three ways to adapt the amount how often a specific component should be considered: * Use addLibraryComponent(LibraryComponentName) several times. * Use updateComponentAmount(LibraryComponentName,AddAmount) adding the second argument to the amount of the specific component. * Use setComponentAmount(LibraryComponentName,Amount) explicitly setting a component’s amount. Moreover, one can define whether synthesis should consider constants that have to be enumerated by the solver by using the method setEnumerateConstants(). If is false, only constants that are in the scope of the currently loaded machine are considered. For instance, if the current machine does not define any integer constant and we want to synthesize a predicate "x + 1 > y" the constraint solver needs to enumerate an integer constant to the value of 1 to achieve the desired behavior. If synthesizing an operation, one can further define whether if-statements should be considered during synthesis represented by the enum ConsiderIfType. There are three possibilities: * NONE: Do not consider if-statements. * EXPLICIT: Use explicit if-then-else expressions as supported by ProB (this might be slow depending on the problem at hand). * IMPLICIT: Do not use explicit if-statements but possibly synthesize several machine operations with appropriate preconditions instead (semantically equivalent to using explicit if-statements in a single machine operation).